On a Researcher's Momentum
One day a coworker casually claimed "As a researcher you have a fixed momentum: if the number of projects you have lowers then you're able to work faster". This is an exploration of his claim.
Every researcher has a fixed momentum
First, the momentum of a particle:
$$p = mv$$
where $m$ and $v$ are the mass and velocity of the particle. If $p$ is constant, then a decrease in $m$ implies an increase in $v$, and vice versa.
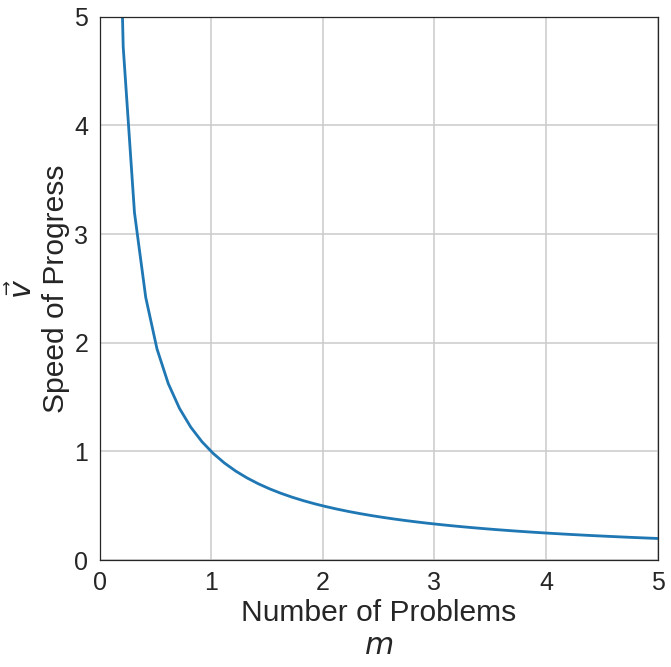
Now, if 'particle' is replaced with 'researcher', a researcher's momentum is the product of the number of problems the researcher is actively tackling and the speed at which they are progressing on the research. This relationship is shown visually for $p=1$ where the inverse relationship between "Number of Problems" and "Speed of Progress" is more obvious.
$$ p = m\vec{v} = \left(\text{Number of Problems}\right)*\left(\text{Speed of Progress}\right)$$
Why problems the researcher is actively tackling? Hamming claims most good researchers have several unsolved problems bouncing around the back of their minds, and I agree. These problems do not add to a researcher's "research mass" because they may only receive an hour or two of thought a year as new pieces of the puzzle arrive. Active problems are those that will receive several hours of attention over the course of a week.
Progress is a little harder to define. It is the very nature of a researcher to tackle problems that are difficult to make progress on! For the sake of this thought experiment, progress will be something along the lines of "making positive strides towards a goal". So a higher velocity implies reaching goals faster.
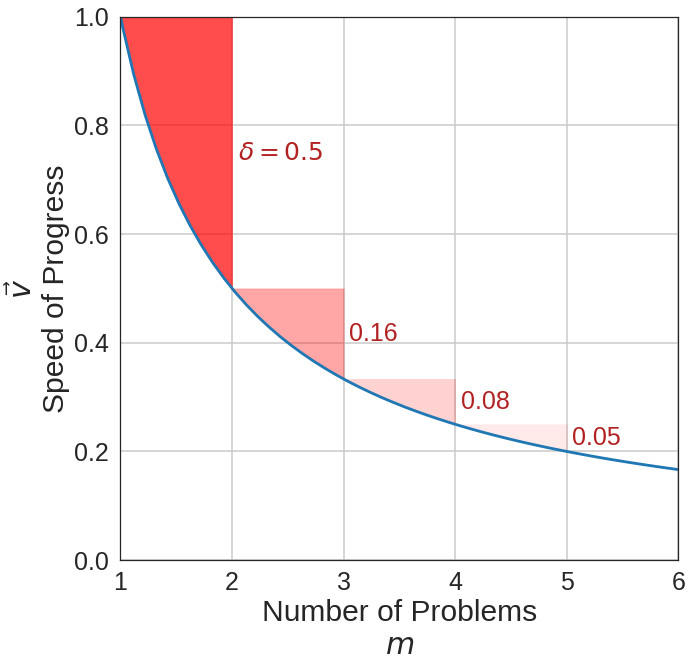
Now, let's take a closer look at the graph, rescaled and annotated below. With one project, a researcher is moving at their nominal fastest speed of 1.0. As soon as a second project is added, speed is reduced by 50%! The researcher may work at half of their top speed for a while then get a third project added to the bunch. This project knocks the velocity down to 0.33, but is only a 16% reduction from the previous speed. Adding a fourth project only reduces the speed by 8%. It seems quite logical that after a second, and especially a third, project are on a researcher's mind the bulk of the speed penalty has been paid and and there is minimal harm in adding more. This is not quite correct.
As any dynamicist reading this will point out: "the derivative of momentum is the sum of external forces, so momentum can't be a constant!" and they would be correct.
$$\dot{p}=\Sigma F_{ext}$$
Probably the most prevalent external force on a moving body (researcher at work) is the force of friction.
$$F=-\mu mg$$
where $\mu$ is the coefficient of friction, $m$ is mass, and $g$ is the acceleration due to gravity. Note that the $F$ is negative thus opposing motion.
How does friction apply to a researcher? It's quite simple: friction is the mental cost of context switching! As $m$ goes up, so does the mental cost of switching from one problem to another! Assuming $\mu$ is constant, a researcher with a low mass and high velocity is inherently better because the mental cost of context switching, and thus the impact on momentum, is smaller.
However, $\mu$ is not a constant by any means, and is unique to each researcher. Some researchers are afflicted (blessed?) with N.A.D.D and have a $\mu$ near 0. That is, all an increase in $m$ does is reduce $v$. The penalty they occur for context switching is marginal. On the other hand, some researchers firmly acknowledge the myth of multitasking and have coefficients of friction much closer to 1. As $m$ goes up, $v$ goes down, and they face penalties from the constant context switching. The impact of $\mu$ is dramatic, as shown below where $1/x-\mu x$ has been plotted for various $\mu$.
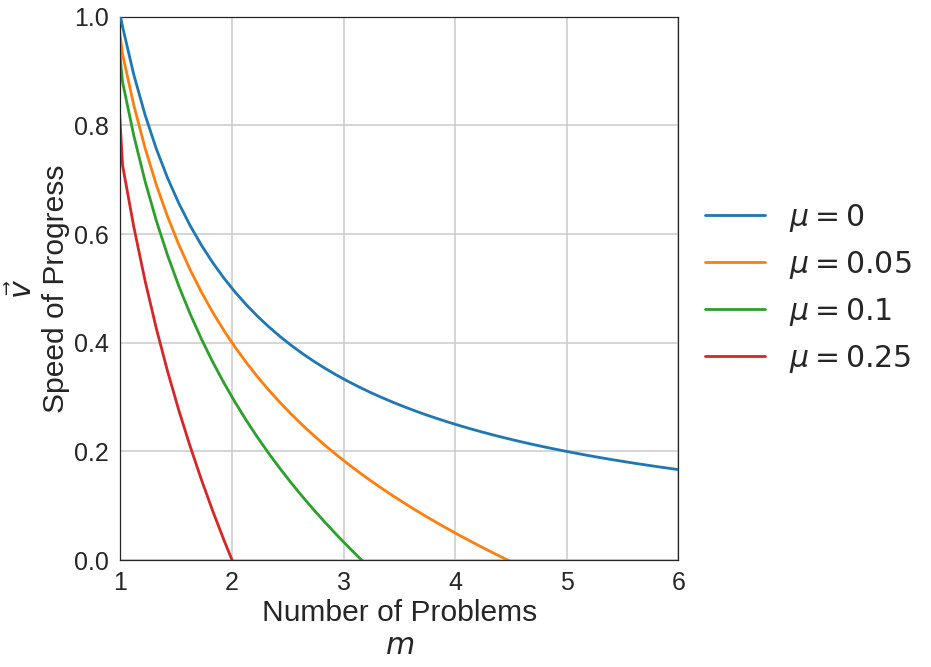
It is important to realize what sort of $\mu$ you have and how that jives with the $m$ and $v$ preferences of your supervisor and teammates.
It should be obvious that the thesis we started with, that a researcher has a constant momentum, is flawed. The proper thesis should be that a researcher has a constant intrinsic momentum. The instrinsic momentum ($p_i=k$) is different than the research momentum $(p_r=p_i+\int\sum F_{ext}=mv)$. Environmental forces directly impact research momentum.
The right combination of external forces can boost research momentum. Ergonomic work spaces, private offices, having the resources you need on hand, supportive teammates, are all ways to bump up an intrinsic momentum with external forces. Having a leader with a vision who removes obstacles before the team hits them is another positive boost. On the other hand, a quality researcher could be ground to a halt by a poor work environment. Copious amounts of red tape, coworkers who don't work (and an interesting rebuke) are all ways to rapidly pull down research momentum. An environment chock-full of negative external forces will rapidly turn into the dead sea and take on a momentum of its own.
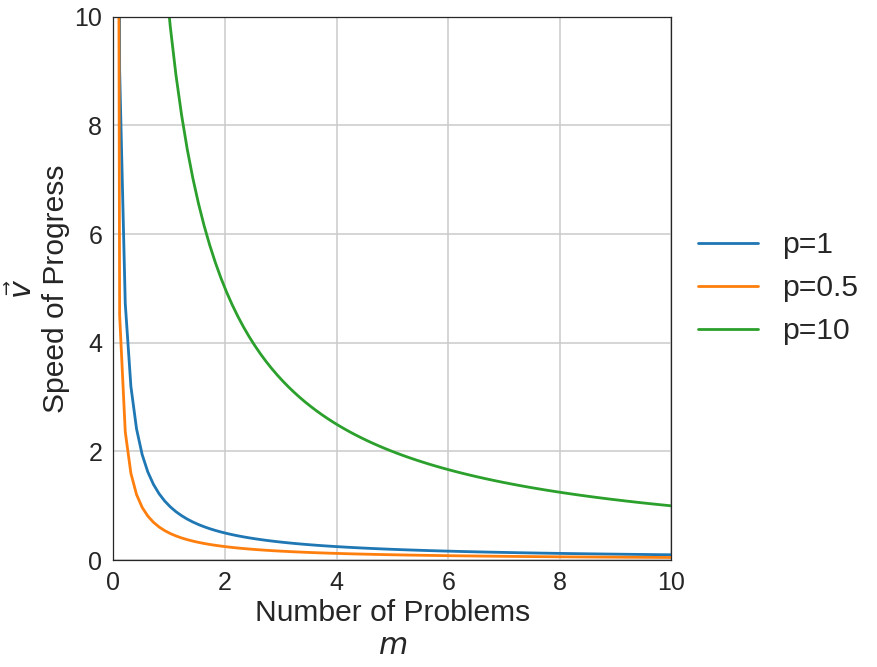
An interesting edge case for this "law" is the 10x engineer. Intrinsic momentum curves for a 0.5x, 1x, and 10x engineer are plotted above. By the virtue of $p=mv$ a 10x engineer will always make 10x the progress of a 1x engineer if they're working on the same number of problems, regardless of the number. An intriguing question arises: can a 10x engineer turn into a 1x engineer in a poor environment? A better way to phrase the question: can a 10x engineer with a relatively high $\mu$ be turned into a 1x engineer through overload? As usual, we turn to plots; the plot from above has been amended with 10x and 1x curves where $\mu=0.1$ has been applied.

Immediately it is obvious that a 1x engineer with negative external forces can be reduced to the level of a 0.5x engineer with neutral forces at $m=2$. Another detail that standouts is that the 10x engineer only performs at a 1x level after they are working on nine different projects. Something about the 10x engineer allows them to persevere and still progress faster than a 1x, even in a negative environment. Another interesting phenomena is that the 10x and 1x engineer suffer the same percentage reduction in speed when the number of problems is changed from two to four. However, in absolute terms, the difference is much more dramatic. The 10x engineer takes a -2.5 progress hit, ten times larger than the 1x engineer (-0.25)! By going from two to four projects, a 10x engineer loses the productivity of two and a half 1x engineers!
Again, this is all conjecture and written for fun. But maybe there's some truth to it. Who would've thought an off-handed hallway comment would have led to this much analysis?
Was this information useful or thought provoking? Do you appreciate a webpage free of analytics or ads? Please consider using my Amazon Affilliate URL as a way of saying thanks. Or, feel free to donate BTC (1DNwgPQMfoWZqnH78yt6cu4WukJa3h8P1f) or ETH (0xf3c4a78c24D34E111f272Ac2AC72b1f01ba52DF3).